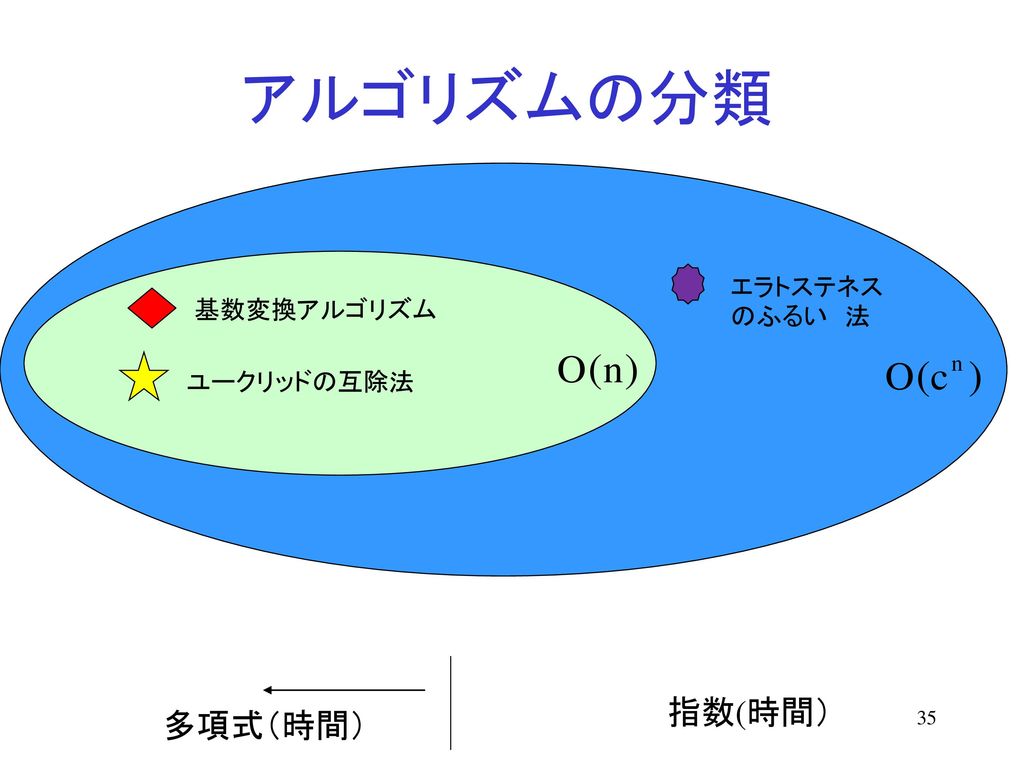
2106 · エラトステネスとは。ギリシアの天文学者,地理学者,詩人。 ヨーロッパでは16世紀にコペルニクスが登場するまで地動説が信じられていましたが、その1700年以上前に地球を球体と考えて、その大きさを測定してしまった人のようです。 エラトステネスwwwyhistorynet 試し割り法を更に効率化 · 今、家にある中学の参考書を読みながら、中学数学を勉強しているものです。その中の素数についての一番最初の問題で、次のうちから、素数を選べ。1 6 13 25 51 79 87 91という問題があり、その解法の一つでエラトステネスのふるい · project C言語でN番目の素数を見つける コードは正常に実行されますが、「forループ」を使用して0000まで反復する代わりに、より良い代替手段がある可能性があり、それを見つけるのに苦労しています。 このソリューションを最適化するために助けが必要

プログラミング
エラトステネスの篩 c言語 高速化
エラトステネスの篩 c言語 高速化-Sieve of Atkinアトキン の篩 より現代的で高速なアルゴリズム カテゴリ: カテゴリ未分類 In mathematics, the sieve of Atkin is a modern algorithm for finding all prime numbers up to a specified integer Compared with the ancient sieve of Eratosthenes, which marks off multiples of primes, the sieve of Atkin doesRecursion 遅い エラトステネスの篩 高速化 エラトステネス計画のふるい (3) 私は、Webでエラトステネス篩の実装についてスキームを探していましたが、多くのコンテンツを考え出しましたが、そのうちのどれもそれを行う必要があるようには思えませんでした。
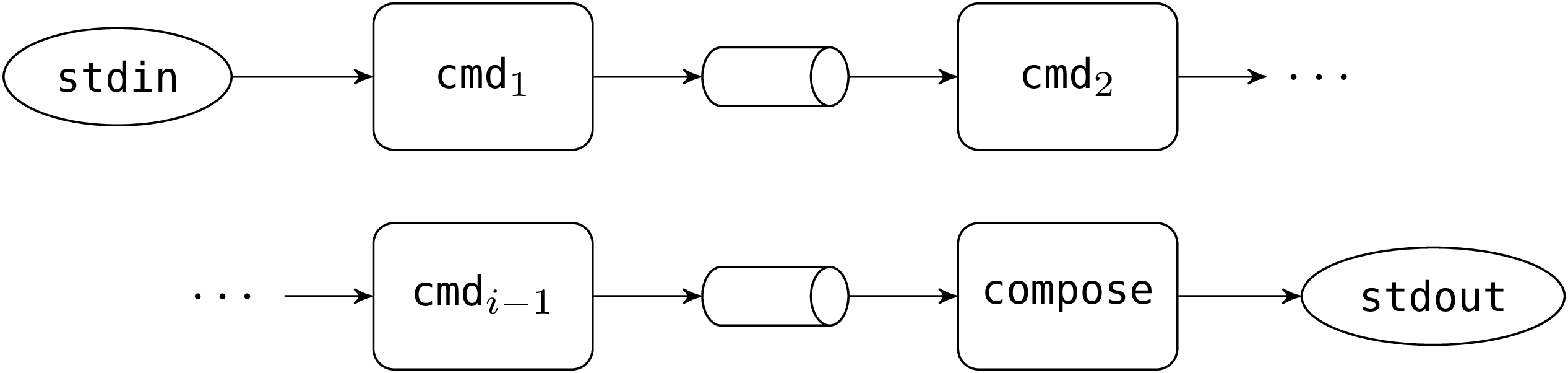



Ocaml による Unix システムプログラミング
2406 · 毎日C言語 5日目 エラトステネスの篩 C言語 今日 ()からアルゴリズムを勉強していこうと思う。 選ばれたのはC言語です。 理由は単純で今勉強中だから。 メモ用として使っていくので詳しい解説はしない (というか知識がないからできない)。 よく · * 素数判定を頑張って高速化してみる エラトステネスの篩編 Apr 14 14 まずはこの問題を見ていただきたい。 · 素数のカウント 高速化 エラトステネスの篩を使ってときました。 ある範囲から素数を見つける c言語 更新
暗号化とは? 素数って実社会でどう使われているの? どのように暗号化するか? ほぼ高速な素因数分解のプログラム; · さすがに C言語で、1億以下の最大の素数でも、だいたい 7秒くらいで計算します(最大の素数のみを出力する場合)。結果は でした。 コンパイルした実行ファイルをアップロードしておきます(Windows用です)。 エラトステネスの篩zipエラトステネスの篩を使って素数探索のプログラムをc言語で作ってみたので投稿します。エラトステネスの篩は 素数に関する私の回答 で紹介しているとおり, 素数の倍数を順につぶしていき, 残った整数を出力するアルゴリズムです。プログラミングのテキストでよく見るアルゴリズムは, 素数
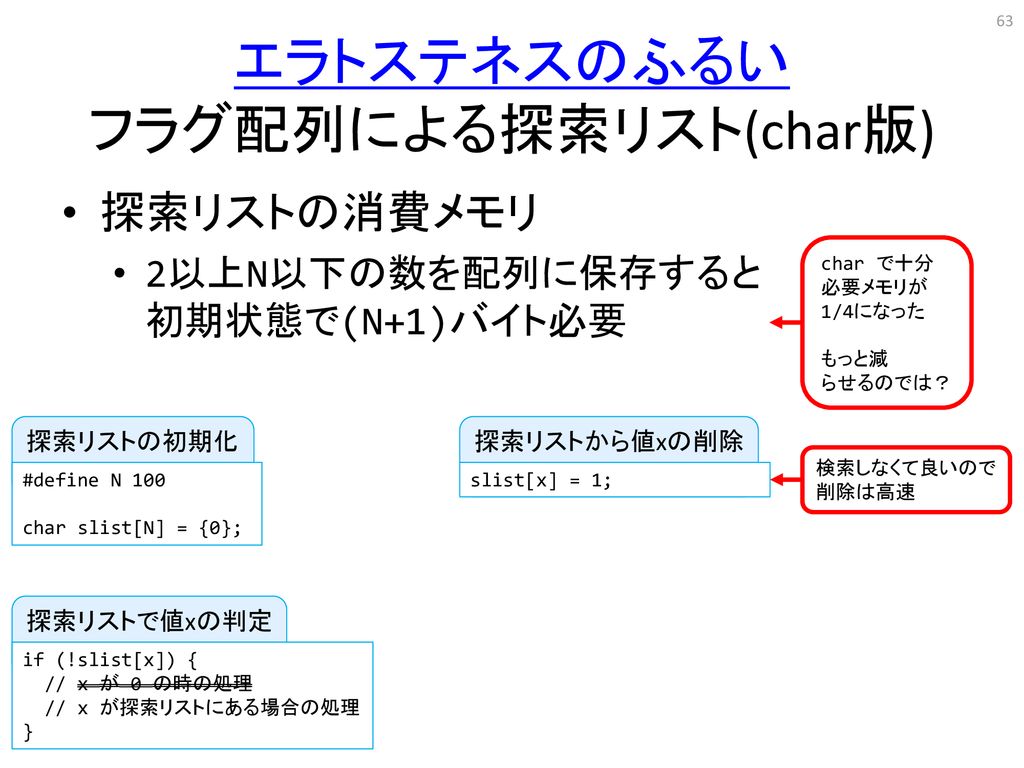
· 素数判定 高速化 素数判定の高速化に挑戦 crayon60d21ed56f/ 高速化できた。現状、ユズノハ史上最速の素数判定。 crayon60d21ed56f/0210 · エラトステネスの篩をC言語で実装 学校の課題で「エラトステネスの篩を用いて100以下のすべての素数とその個数を表示するプログラムを作成せよ。 」との課題が出題されたのですが、ヒントを読むなり先生からの説明を聞くなりして、原理は理解できた · c エラトステネスのふるい! Updated 1805 00 今日は、2 以上 n 以下の自然数の中から素数を抽出(素数以外を排除)する C によるアルゴリズムについてです。




Ocaml による Unix システムプログラミング



Ocaml による Unix システムプログラミング
第 1 章で、C言語のプログラム中では、 " (ダブルクオーテーション)で囲まれた文字の並びが文字列だと説明しました。実はC言語では、文字列は char 型の配列の一種です。これが何を意味するか、以下で詳しく見てゆきます。24 · エラトステネスのふるいとその計算量 エラトステネスの篩そのもののの高速化についてはこちらで検討しました。 ここでは純粋に for 文と while 文の比較を行います。 Python でエラトステネスの篩 # 431 比較対象 比較対象は、次の通りです。 · C言語でアトキンの篩を実装したい〈初心者〉 この春から大学でプログラムを学び始めた者です。 講義にて、素数の演算と表示に関する話がありました。 その中で、エラトステネスの篩とアトキンの篩について紹介があり、どちらの方がどのくらい早いの
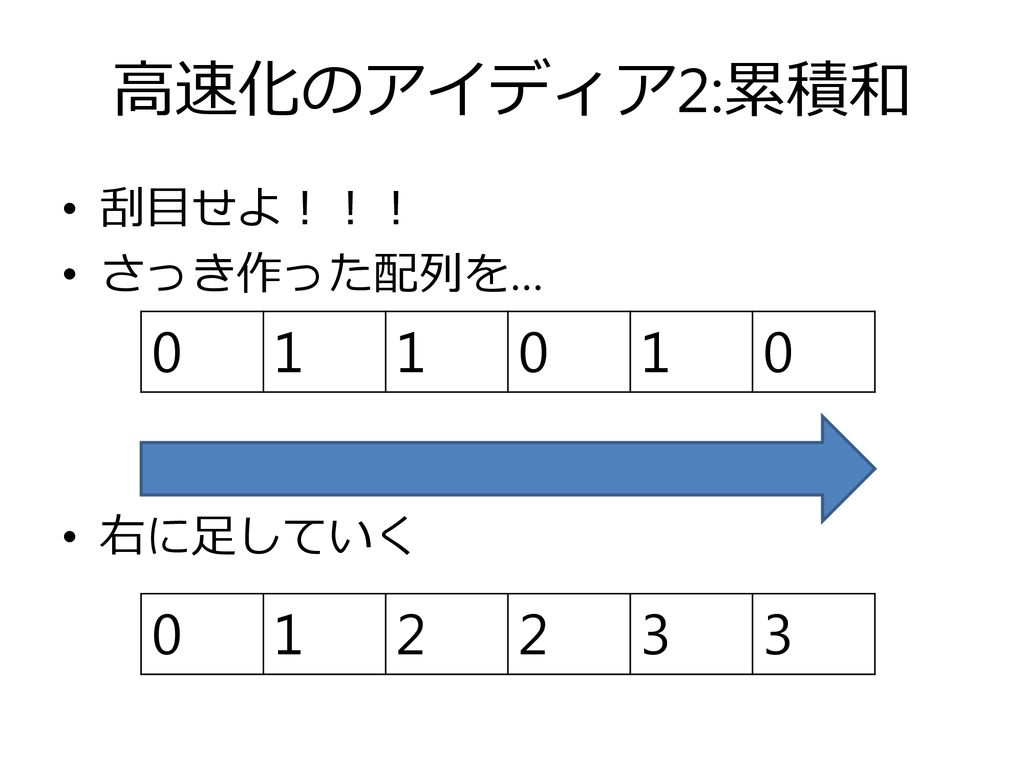



Kagamiz Jayson Sho Toma Ppt Download




Ducalog Tumblr Blog Tumgir
1002 · コードの間違い探し問題(C言語) 久しぶりに素数が見たいと思い、素数列挙のアルゴリズム、エラトステネスのふるいをC言語で書いた。 その際絶妙な間違いを犯した。 その間違いを探してみてほしい。 整数をそれぞれその整数の平方根以下の素数で · エラトステネスのふるい: n n n 以下の素数を全て見つけ出す高速な方法。 エラトステネスの篩(ふるい)の概要と,愚直に計算するよりも速いこと(計算量が O ( n log log n) O (n\log\log n) O(nloglogn) であること)を解説します。 目次 愚直な方法 · エラトステネスの篩は、速いアルゴリズムらしいです。 とりあえずエラトステネスのふるいの方が速いことを理解しておいてください。 エラトステネスのふるいとその計算量 エラトステネスの篩そのもののの高速化についてはこちらで検討しました



Topcoderでプログラムしてみた




アルゴリズムでいこう 素数 エラトステネスのふるい Donguri Note
0617 · ここでの条件 C言語で実装 エラトステネスの篩を使う 素数の数を求める(100 なら 25) コンパイラ最適化とかパイプラインとかには適度に期待する 最大値はそれなりに小さいとする 計算時間は手元の Mac で測っている(コンパイラは clangリスト 高速化 def solver1(n) primes = 2, 3 x エラトステネスの篩 他のプログラミング言語では、この方法でも高速に実行できるかもしれません。興味のある方は試してみてください。そもそも「エラトステネスの篩」自体が素数探索の高速なアルゴリズムであるので、実質、Cでの効率的な実装は?という質問に置き換えられると思います。 プログラミングという魔法を学ぼうというスペースでモデレータをお願いしている Tokieda Yukinobuさんが投稿された 素数探索
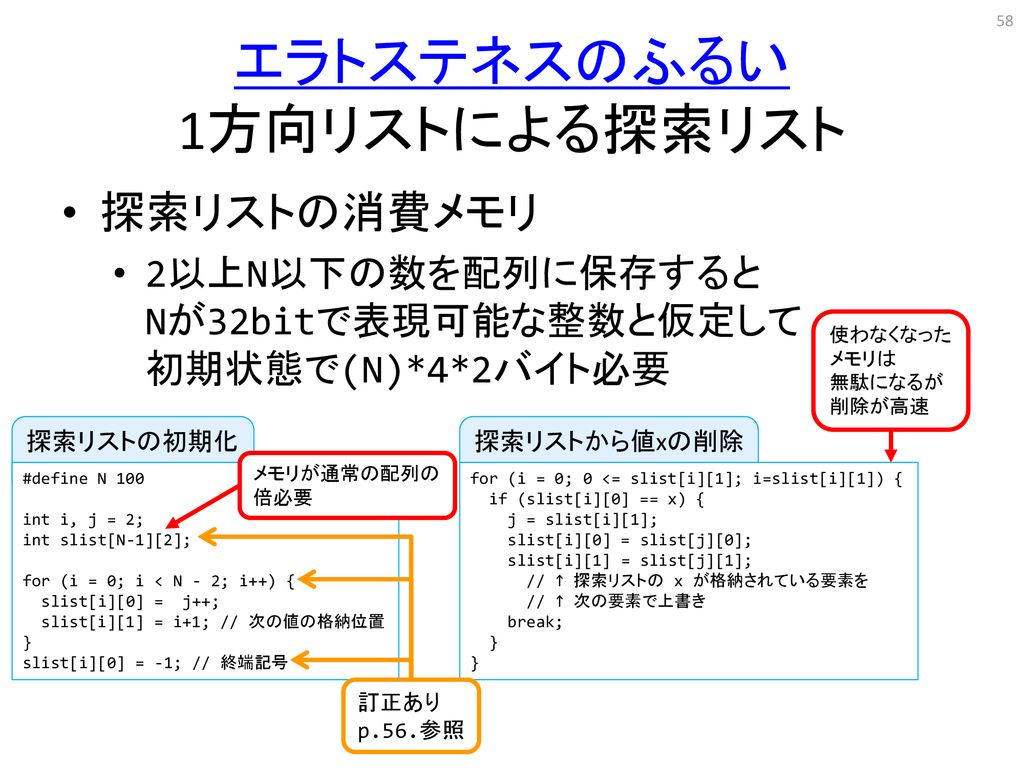



プログラミング言語 実習を含む 計算機言語 計算機言語演習 情報処理言語 実習を含む Ppt Download



Topcoderでプログラムしてみた
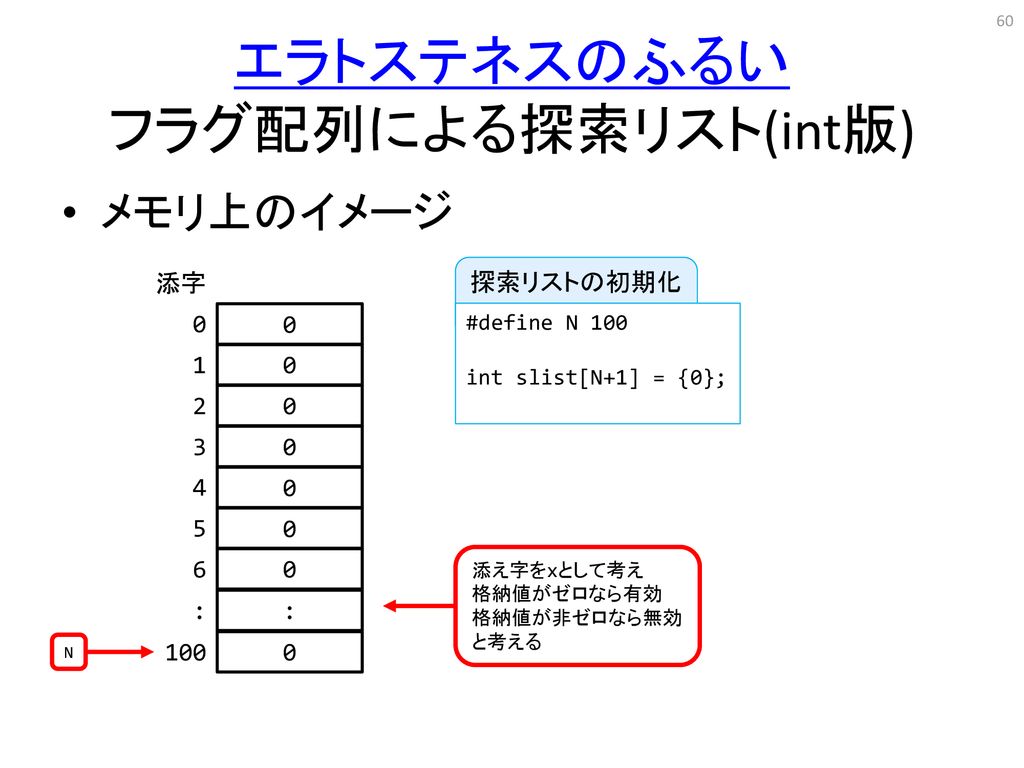
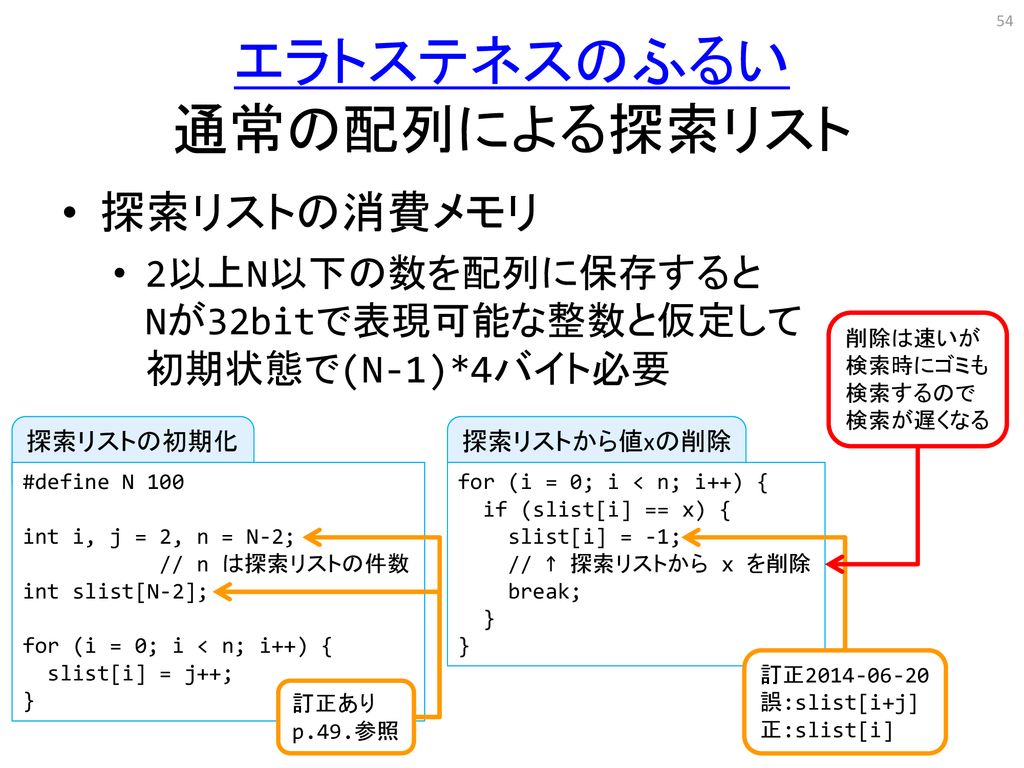
古い規格のC言語では、for 文の初期化で変数を宣言することはできません。 リスト エラトステネスの篩 (sample27c) #include #include #define N 100 // false は素数, true は素数ではない bool primes · Project Eulerのとある問題でエラトステネスの篩を高速化している人がいた。 なかなか興味深かったので、コードを読みといて自分なりにアレンジしてみた。 ローカル環境で約2倍の高速化に成功した。1e8までのふるいが07s程度で実行出来た。 普通のふるい1102 · for loop エラトステネスのふるい:C言語 すべての要素を 1 で初期化する 。どうして? print_prim を見ているから 、1に等しい値を出力します。したがって、すべての素数を2シフトし、その値を 1 にする必要があります。



Linuxmint アトリエコムコム




100万ドルの問題 アルゴリズムとグラフ理論 Ppt Download
· プログラミングを学びたての頃に素数を羅列するプログラムを書いていたのでここにも貼っておこうと思います。 その時は知らなかったのですがエラトステネスの篩(ふるい)という素数を探すアルゴリズムがあるみたいですね。 これも実装しましたので下に書いておきます。 使用言語 · エラトステネスの篩は素数を見つけるためのアルゴリズムとしてよく知られているものです 複数の素数を列挙する場合には、試し割りによる方法よりも高速に処理できます どのようなアルゴリズムかという以下の画像がわかりやすいです この43 エラトステネスの篩 # 3 OrderedDict # 背景 枝狩りをした 2 高速版のアルゴリズムでも、 既に素数でないと判定されたものにも重複して、素数でないと判定しています。 同じ j に対して複数回 is_primej = False を実行しています。




アルゴリズム Atcoder のための数学 中編 数学的知識編 Qiita




技術書典7に Haskellで競技プログラミングをやる本を出します 雑記帳
· エラトステネスの篩の素数判定プログラム (c#) スポンサーリンク ※サイト運営にサーバーは 必須 です※ ~このサイトも エックスサーバー を使用しています~ 目次 hide 1 はじめに 2 1:単純なエラトステネスのふるい 3 2:√Nで、篩を止める 4 3奇数例 1 素数表の作成(エラトステネスの篩(sieve)) 配列を用いたプログラムの例として, エラトステネスの篩法で 素数表を作成します エラトステネスの篩は, 小さい素数から順に その数の倍数を消去していくことにより素数を残していく方法で, とても効率が良い事が知られています0301 · 素数判定で、高速化って調べると、だいだい検索に出てくるやつです。 エラトステネスの篩 (エラトステネスのふるい、 英 Sieve of Eratosthenes) は、指定された 整数 以下の全ての 素数 を発見するための単純な アルゴリズム である。 古代ギリシア の科学者




記事一覧 Oucrc 岡山大学電子計算機研究会




Ducalog Tumblr Blog Tumgir
0508 · 素数判定を使うことが多いProject Eulerなので、Problem 6,Problem 10の回答例を見ながら試し割りの高速化を図ります。 試し割り編 今までのアルゴリズムは、2以外の素数は奇数。というルールに基づき、3から3,5,7,9,11,13と偶数で割ってみて√2まで割り切れなければ素数。高速化 関数 遅い 速度 素数 コード エラトステネスの篩 エラトステネスのふるい エラトステネス アルゴリズム ふるい c言語 algorithm haskellエラトステネスの篩 (エラトステネスのふるい、英 Sieve of Eratosthenes) は、指定された整数以下の全ての素数を発見するための単純なアルゴリズムである。 古代ギリシアの科学者、エラトステネスが考案したとされるため、この名がついている。



100万ドルの問題 アルゴリズムとグラフ理論 Ppt Download




19年6月日 Sakurai Susumu Website



アルゴリズム Pukiwiki




プログラミング




プログラミング




素数発見アルゴリズム エラトステネスのふるいはどのくらい速いのか Gota Morishita Note




19年6月日 Sakurai Susumu Website




N Iとは ウェブの人気 最新記事を集めました はてな



記事




Ocaml による Unix システムプログラミング




アルゴリズム Atcoder のための数学 中編 数学的知識編 Qiita




プログラミング言語 実習を含む 計算機言語 計算機言語演習 情報処理言語 実習を含む Ppt Download




C プログラミング入門 19 第12回 4 演習 Complex Sieve Youtube




Kagamiz Jayson Sho Toma Ppt Download




禁則事項 民主主義に乾杯




Atcoderに便利なサイト 拡張機能まとめ ながめも



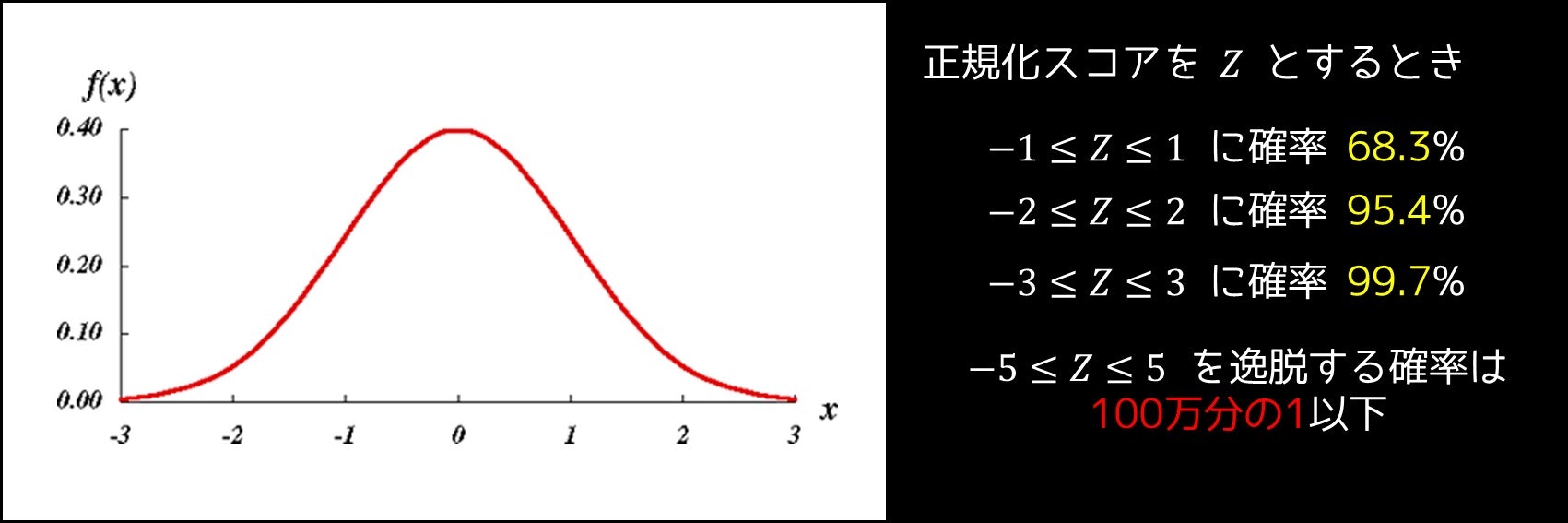
アルゴリズム Atcoder のための数学 中編 数学的知識編 Qiita




情報科学 18




100万ドルの問題 アルゴリズムとグラフ理論 Ppt Download




フェルマーの小定理とは サイエンスの人気 最新記事を集めました はてな




玉川テラス Sakurai Susumu Website



Python のコードを最適化したい 民主主義に乾杯




Atcoder での実力アップを目指そう 競プロ典型 90 問 Qiita




ページ 9 Sakurai Susumu Website




プログラマを育てる脳トレパズル 遊んでおぼえるpythonプログラミング アルゴリズム Seshop Com 翔泳社の通販




ソフトウェア シンポジウム 16 In 米子 論文集



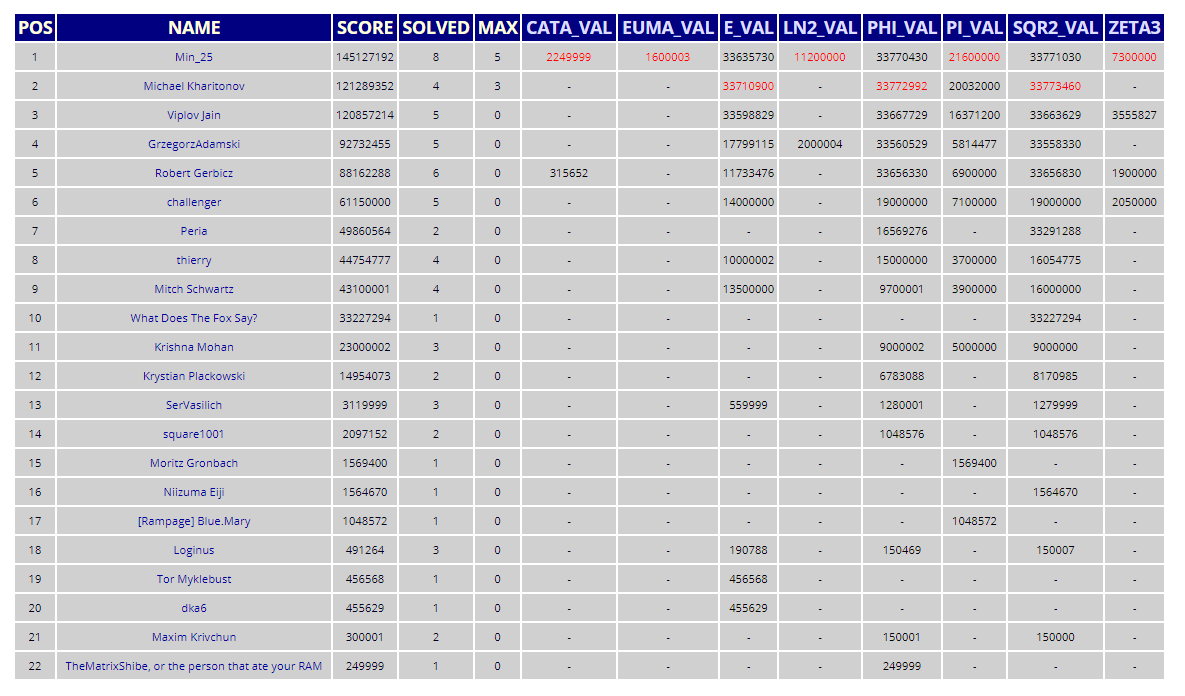
超高速 多倍長整数の計算手法 後編 N の計算から円周率 100 万桁の挑戦まで Qiita



プログラミング言語 実習を含む 計算機言語 計算機言語演習 情報処理言語 実習を含む Ppt Download




素数判定のエラトステネスの篩はどれぐらい速いんすかね Ts0818のブログ



Atcoder Educationaldpcontest O Matchingをrubyで解く




Atcoder での実力アップを目指そう 競プロ典型 90 問 Qiita




Ocaml による Unix システムプログラミング




Kagamiz Jayson Sho Toma Ppt Download




プログラミング




N Iとは ウェブの人気 最新記事を集めました はてな




100万ドルの問題 アルゴリズムとグラフ理論 Ppt Download




ページ 9 Sakurai Susumu Website




プログラミング言語 実習を含む 計算機言語 計算機言語演習 情報処理言語 実習を含む Ppt Download



Leetcodeを使い倒す 初級編




年3月3日 Sakurai Susumu Website




Ducalog Tumblr Blog Tumgir



Jig 福野泰介の一日一創 Create Every Day By Taisuke Fukuno



Bt 5527 品番 Bc4 会議用テーブル Inb 文具の月島堂 Bt 5527 ナチュラルメープル オフィス家具 会議用テーブル Bt 5527 全国配送可 イナバ




君はインド式計算を知っているか Sakurai Susumu Website




Python のコードを最適化したい 民主主義に乾杯



Jigintern 福野泰介の一日一創 Create Every Day By Taisuke Fukuno




民主主義に乾杯




アルゴリズム Atcoder のための数学 中編 数学的知識編 Qiita




年1月 Sakurai Susumu Website



プログラミング言語 実習を含む 計算機言語 計算機言語演習 情報処理言語 実習を含む Ppt Download



Exercise Of Programming For Numerical Methods



プログラミング言語 実習を含む 計算機言語 計算機言語演習 情報処理言語 実習を含む Ppt Download



一条蛍 Tumblr Posts Tumbral Com




Ocaml による Unix システムプログラミング




Atcoderで水色になるまでにやったこと ながめも




Python のコードを最適化したい 民主主義に乾杯




Kagamiz Jayson Sho Toma Ppt Download




Zdd Zero Suppressed Binary Decision Diagram ってものが存在するそうな Ts0818のブログ



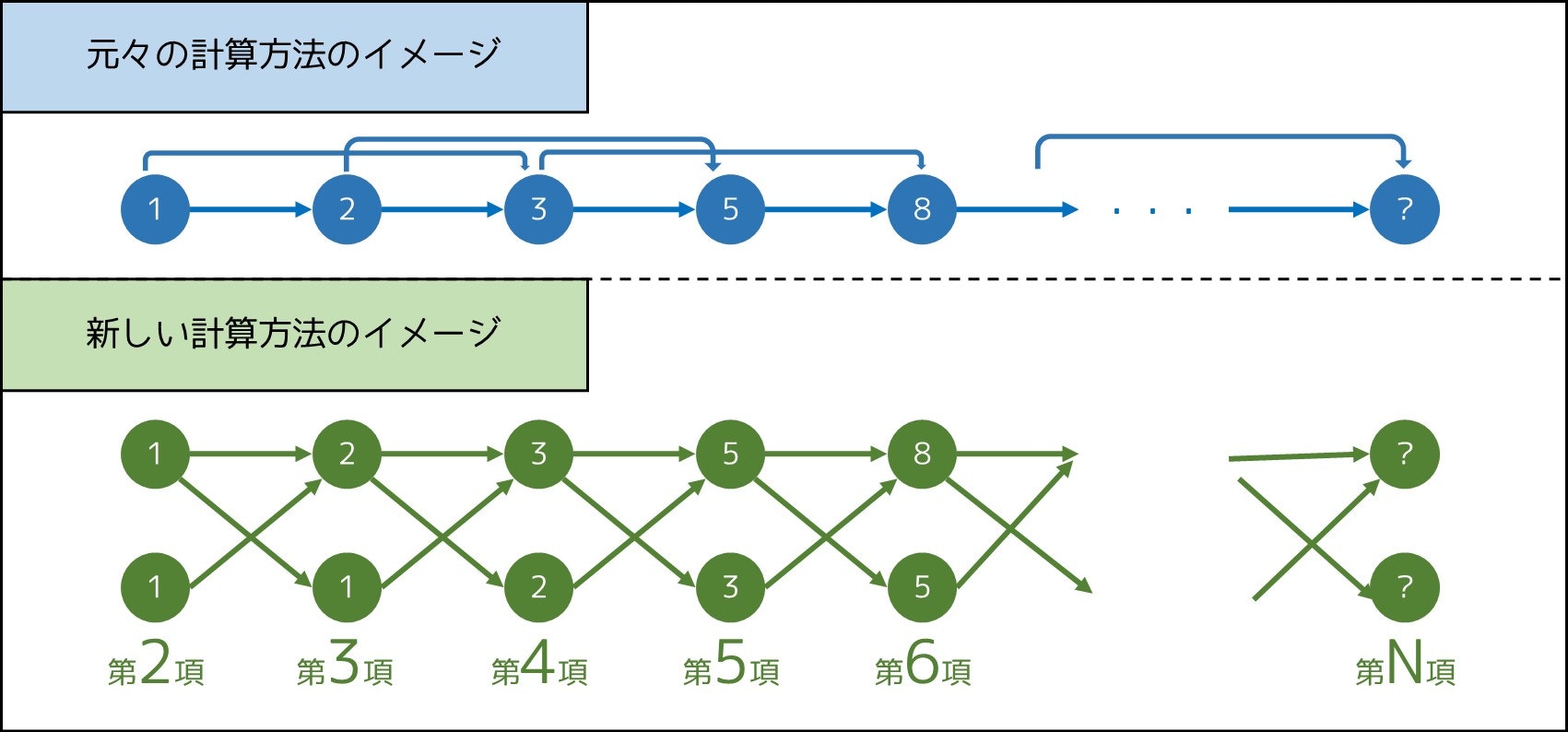
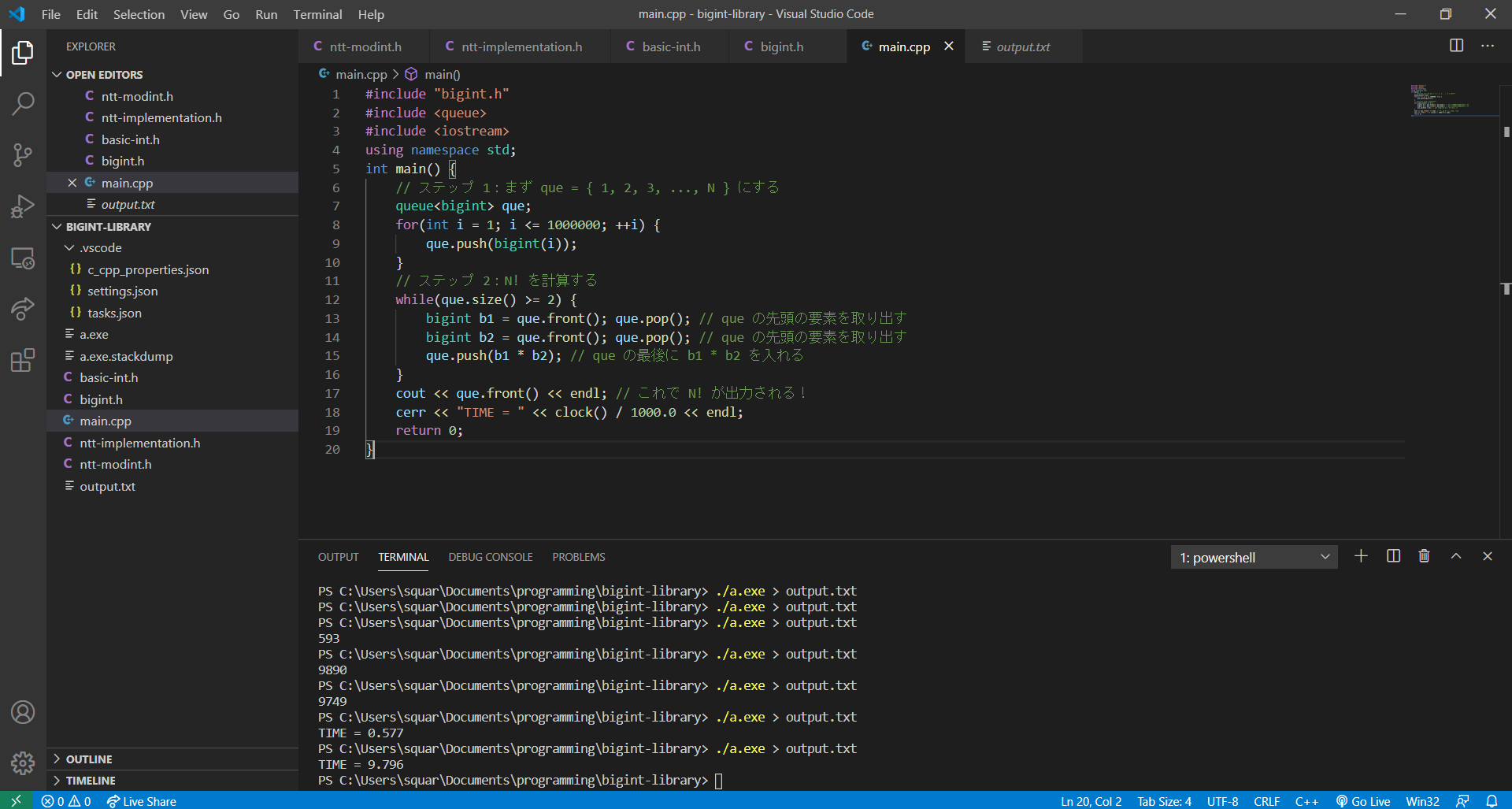
超高速 多倍長整数の計算手法 後編 N の計算から円周率 100 万桁の挑戦まで Qiita



アルゴリズム Atcoder のための数学 中編 数学的知識編 Qiita



0 件のコメント:
コメントを投稿